백준 9251번 - LCS

문제

백준 9251번 문제
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.

예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.

입력

첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.

출력

첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를 출력한다.

예제 입력 1 복사

ACAYKP
CAPCAK

예제 출력 1 복사

4

풀이

테이블과 테이블에서 점화식을 유추해내는 것이 어려움
우선 점화식을 위한 테이블을 정의하고 채워야하는데 해당 부분이 어렵다
부분집합을 단순히 생각하면 각 단어의 부분집합의 가짓수가 많기 때문에 시간복잡도에서 안됨

테이블을 작성해야되는데 문자열과 문자열을 비교해야 하므로
결국 2중for문을 사용해야하고 $O(n^2)$의 시간복잡도가 걸리며 2차원테이블을 작성해야 함

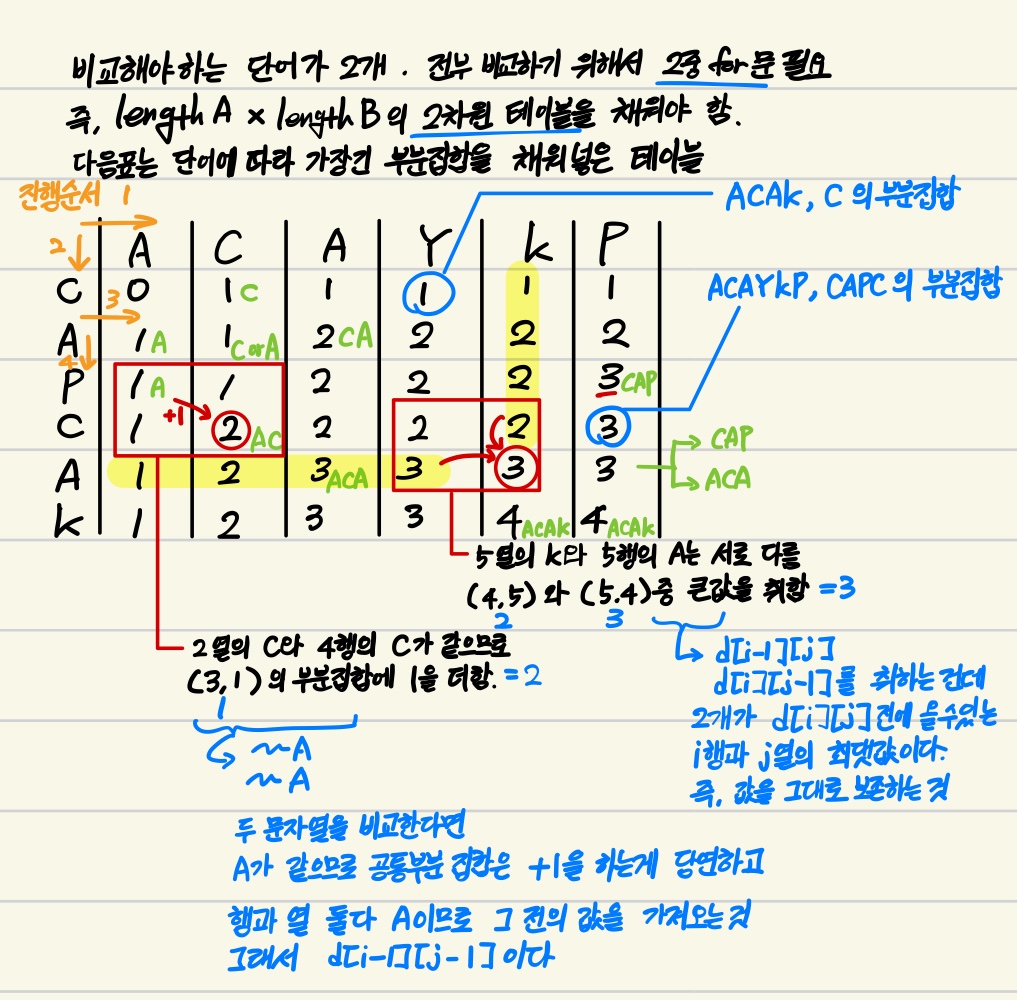
표를 작성한 뒤 법칙성을 찾아서 점화식을 뽑을 수 있는데
서로 같은 단어가 왔을 때와 다른 단어가 왔을 때를 나누어야 함

서로 글자가 같을 때
d[i][j] = d[i-1][j-1] + 1

서로 글자가 다를 때
d[i][j] = max(d[i-1][j], d[i][j-1])

#include <bits/stdc++.h>
using namespace std;

int d[1005][1005];	//d[i][j] : a단어의 i번째, b단어의 j번째에서 공통 부분 수열 중 가장 긴 것

int main(void) 
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	string a, b;
	cin >> a >> b;

	int len_a = a.length();
	int len_b = b.length();

	for (int i = 1; i <= len_a; i++) 
	{
		for (int j = 1; j <= len_b; j++) 
		{
			if (a[i - 1] == b[j - 1]) 
				d[i][j] = d[i - 1][j - 1] + 1;
			else 
				d[i][j] = max(d[i - 1][j], d[i][j - 1]);
		}
	}
	cout << d[len_a][len_b];
}