백준 4883번 - 삼각 그래프

문제

백준 4883번 문제
이 문제는 삼각 그래프의 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최단 경로를 찾는 문제이다.

삼각 그래프는 사이클이 없는 그래프로 N ≥ 2 개의 행과 3열로 이루어져 있다. 삼각 그래프는 보통 그래프와 다르게 간선이 아닌 정점에 비용이 있다. 어떤 경로의 비용은 그 경로에서 지나간 정점의 비용의 합이다.

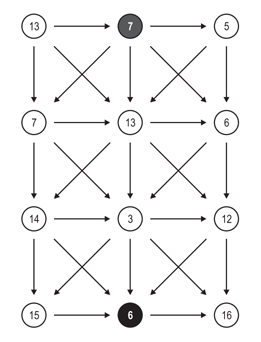
오른쪽 그림은 N = 4인 삼각 그래프이고, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 경로 중 아래로만 가는 경로의 비용은 7+13+3+6 = 29가 된다. 삼각 그래프의 간선은 항상 오른쪽 그림과 같은 형태로 연결되어 있다.

입력

입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 그래프의 행의 개수 N이 주어진다. (2 ≤ N ≤ 100,000) 다음 N개 줄에는 그래프의 i번째 행에 있는 정점의 비용이 순서대로 주어진다. 비용은 정수이며, 비용의 제곱은 1,000,000보다 작다.

입력의 마지막 줄에는 0이 하나 주어진다.

출력

각 테스트 케이스에 대해서, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최소 비용을 테스트 케이스 번호와 아래와 같은 형식으로 출력한다.

k. n

k는 테스트 케이스 번호, n은 최소 비용이다.

예제 입력 1 복사

4
13 7 5
7 13 6
14 3 12
15 6 16
0

예제 출력 1 복사

1. 22

풀이

각 정점에 올 수 있는 가짓수를 계산해보면 된다
첫째줄은 예외로 두고 둘째줄부터 다음과 같은 공식이 성립

d[i][0] = d[i-1][0], d[i-1][1] 중 최솟값 
d[i][1] = d[i-1][0], d[i-1][1], d[i-1][2], d[i][0] 중 최솟값
d[i][2] = d[i-1][1], d[i-1][2], d[i][1] 중 최솟값

2번째 줄부터 한 노드에 몇개의 화살표가 꽂히는지 그림에서 잘 확인해보자

#include <bits/stdc++.h>
using namespace std;

const int mx = 100005;
int arr[mx][3];
int d[mx][3];

int main(void) 
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	int t = 0;
	int n;
	while (true)
	{
		cin >> n;
		if(n == 0)
			break;
		

		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < 3; j++)
				cin >> arr[i][j];
		}

		d[0][0] = 0x3f3f3f3f;
		d[0][1] = arr[0][1];
		d[0][2] = arr[0][1] + arr[0][2];
		for (int i = 1; i < n; i++)
		{
			d[i][0] = arr[i][0] + min(d[i - 1][0], d[i - 1][1]);
			d[i][1] = arr[i][1] + min({ d[i - 1][0], d[i - 1][1], d[i - 1][2], d[i][0] });
			d[i][2] = arr[i][2] + min({ d[i - 1][1], d[i - 1][2], d[i][1] });
		}
		
		cout << ++t << ". ";
		cout << d[n - 1][1] << "\n";
	}
}