백준 2302번 - 극장 좌석

문제

백준 2302번 문제
어떤 극장의 좌석은 한 줄로 되어 있으며 왼쪽부터 차례대로 1번부터 N번까지 번호가 매겨져 있다. 공연을 보러 온 사람들은 자기의 입장권에 표시되어 있는 좌석에 앉아야 한다. 예를 들어서, 입장권에 5번이 쓰여 있으면 5번 좌석에 앉아야 한다. 단, 자기의 바로 왼쪽 좌석 또는 바로 오른쪽 좌석으로는 자리를 옮길 수 있다. 예를 들어서, 7번 입장권을 가진 사람은 7번 좌석은 물론이고, 6번 좌석이나 8번 좌석에도 앉을 수 있다. 그러나 5번 좌석이나 9번 좌석에는 앉을 수 없다.

그런데 이 극장에는 “VIP 회원”들이 있다. 이 사람들은 반드시 자기 좌석에만 앉아야 하며 옆 좌석으로 자리를 옮길 수 없다.

오늘 공연은 입장권이 매진되어 1번 좌석부터 N번 좌석까지 모든 좌석이 다 팔렸다. VIP 회원들의 좌석 번호들이 주어졌을 때, 사람들이 좌석에 앉는 서로 다른 방법의 가짓수를 구하는 프로그램을 작성하시오.

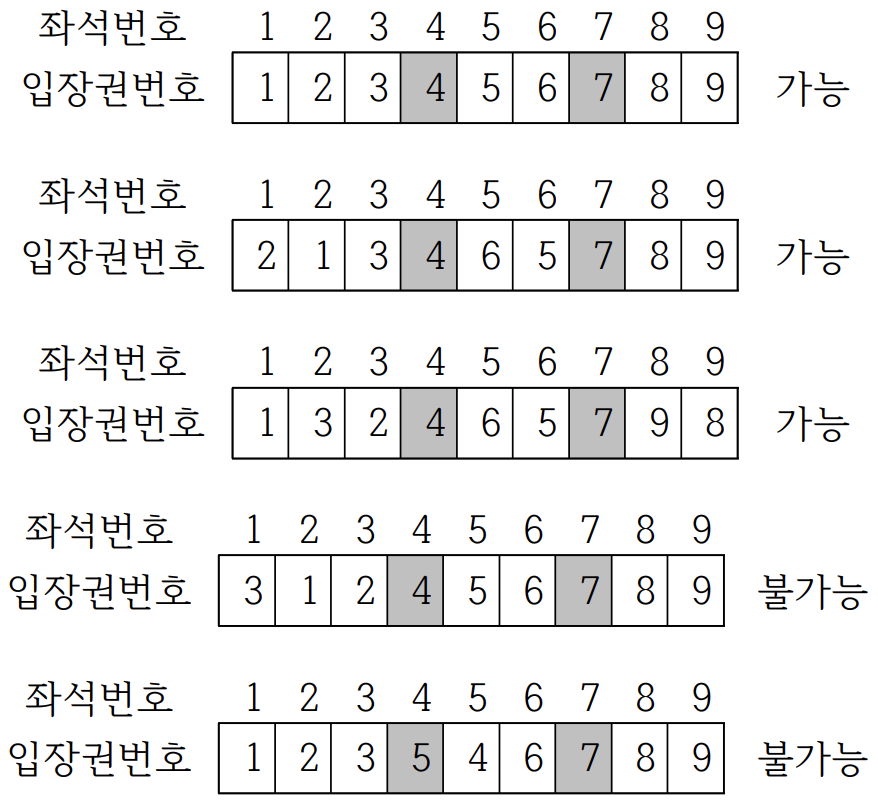
예를 들어서, 그림과 같이 좌석이 9개이고, 4번 좌석과 7번 좌석이 VIP석인 경우에 <123456789>는 물론 가능한 배치이다. 또한 <213465789> 와 <132465798> 도 가능한 배치이다. 그러나 <312456789> 와 <123546789> 는 허용되지 않는 배치 방법이다.

입력

첫째 줄에는 좌석의 개수 N이 입력된다. N은 1 이상 40 이하이다. 둘째 줄에는 고정석의 개수 M이 입력된다. M은 0 이상 N 이하이다. 다음 M 개의 줄에는 고정석의 번호가 작은 수부터 큰 수의 순서로 한 줄에 하나씩 입력된다.

출력

주어진 조건을 만족하면서 사람들이 좌석에 앉을 수 있는 방법의 가짓수를 출력한다. 방법의 가짓수는 2,000,000,000을 넘지 않는다. (2,000,000,000 < 231-1)

예제 입력 1 복사

9
2
4
7

예제 출력 1 복사

12

풀이

전체 n의 개수가 늘어났을 때 어떤 법칙으로 경우의 수가 달라지는지 알아야 함
직접 계산을 해보면
d[1] = 1
d[2] = 2
d[3] = 3
d[4] = 5
d[5] = 8 순으로 진행하게 되는데
이를 봤을 때 피보나치 수열임을 알 수 있다.

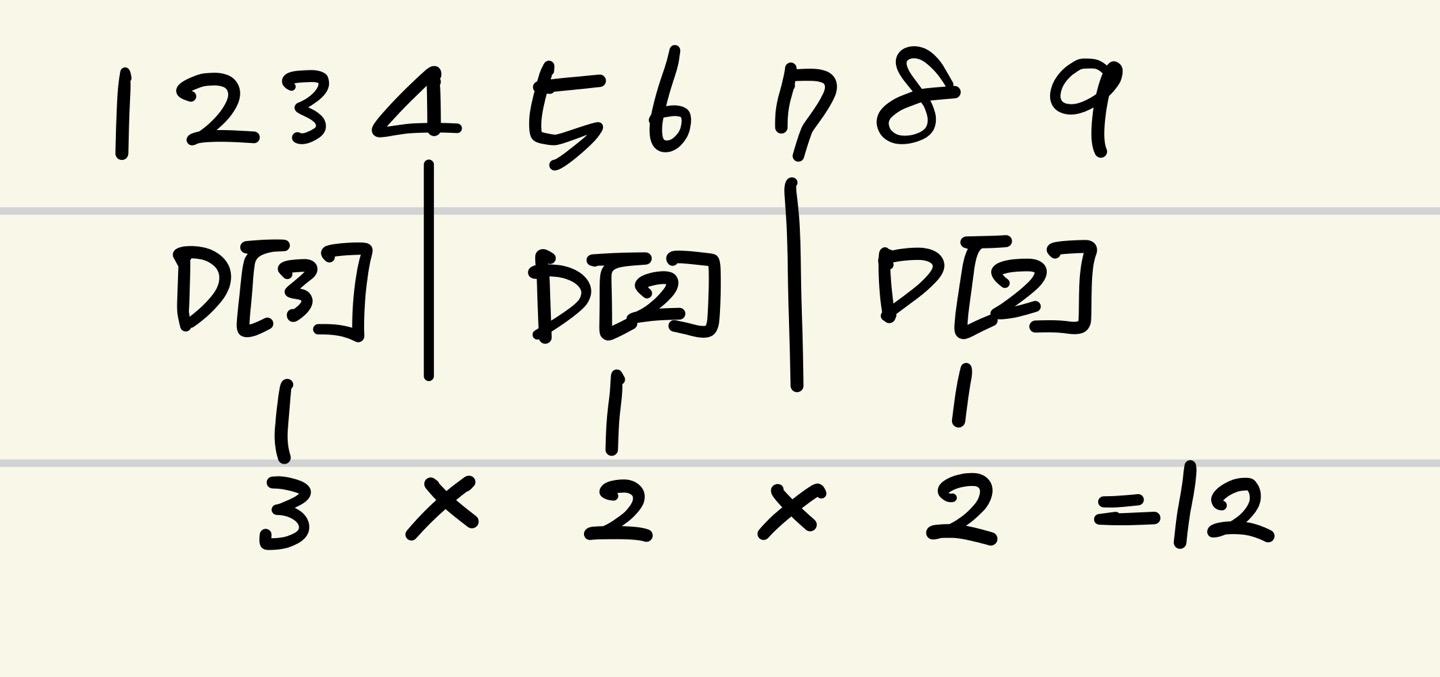
그 뒤에는 중간에 있는 고정석들을 어떻게 처리할 지가 문제인데
고정석 사이사이를 또다른 dp로 봐서
합산은 경우의 수 처리를 위해 곱셈으로 해주면 답을 구할 수 있음

#include <bits/stdc++.h>
using namespace std;

int d[42];	//d[i] : 자리가 i개일 때 경우의 수
int arr[42];
int n;

int main(void) 
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	int m;
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
		cin >> arr[i];

	//초기값 정하기
	d[0] = 1;	//기본적으로 쓰이진 않지만 밑에서 ans에 곱셈연산을 하기 때문에 0초기화 방지를 위함
	d[1] = 1;
	d[2] = 2;
	//테이블 채우기(피보나치)
	for (int i = 3; i <= 40; i++)
		d[i] = d[i - 1] + d[i - 2];

	/*
	* n = 9이고 arr에 4 7이 들어왔다면
	* 정답은 1~3 + 5~6 + 8~9 인데 이는 d[3] * d[2] * d[2] (경우의 수므로 곱셉연산)
	* 아래는 cnt를 세면서 사이수를 구해서 곱하는 연산
	*/
	int ans = 1;
	int cnt = 0, idx = 1;
	for (int i = 1; i <= n; i++)	
	{
		if (i >= arr[idx] && idx <= m)
		{
			ans *= d[cnt];
			cnt = 0;
			idx++;
			continue;
		}
		cnt++;
	}
	ans *= d[cnt];
	cout << ans;
}

다른풀이

#include <bits/stdc++.h>
using namespace std;

vector<int> v = { 0 }; // 고정석의 번호
int d[45]; // 연속된 자리의 개수가 i개일 때 앉을 수 있는 경우의 수

int main(void) 
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	int n, m, vv;
	cin >> n;
	cin >> m;
	while (m--) 
	{
		cin >> vv;
		v.push_back(vv);
	}
	v.push_back(n + 1);	//아래 정답을 구하는 방식에서 사용하기 위해서 마지막 인덱스 삽입

	d[0] = 1;
	d[1] = 1;
	d[2] = 2;
	for (int i = 3; i <= n; i++) 
		d[i] = d[i - 1] + d[i - 2];

	int ans = 1;
	for (int i = 1; i < v.size(); i++) 
		ans *= d[v[i] - v[i - 1] - 1];
	cout << ans;
}
/*
앉을 수 있는 경우의 수는 마지막 자리에 i번이 앉거나 마지막에서 두번째 자리부터 차례대로
i번과 i - 1번이 앉는 두 가지 경우밖에 없으므로 d[i] = d[i - 1] + d[i - 2]이 되어 피보나치 수열을 이룸
*/