백준 11057번 - 오르막 수

문제

백준 11057번 문제
오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다.

예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다.

수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.

입력

첫째 줄에 N (1 ≤ N ≤ 1,000)이 주어진다.

출력

첫째 줄에 길이가 N인 오르막 수의 개수를 10,007로 나눈 나머지를 출력한다.

예제 입력 1 복사

1

예제 출력 1 복사

10

예제 입력 2 복사

2

예제 출력 2 복사

55

예제 입력 3 복사

3

예제 출력 3 복사

220

풀이

쉬운 계단 수 문제처럼 2차원 배열로 접근

#include <bits/stdc++.h>
using namespace std;

using ll = long long;
ll d[1005][11];	//d[i][j] : i번째 자릿수의 자연수(0~9) j가 가질 수 있는 오르막 수
int n;

int main(void)
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	
	cin >> n;

	//테이블 초기값 설정 (첫번재 자리는 자연수 1개씩만 가능하므로 10개)
	for (int i = 0; i < 10; i++)
		d[1][i] = 1;

	//테이블 채우기
	for (int i = 2; i <= n; i++)
	{
		for (int j = 0; j < 10; j++)	//자연수 0~10 까지 채우는 과정
		{
			int idx = 9;
			while (idx >= j)	//j보다 같거나 작은 값의 이전 테이블을 전부 더함
				d[i][j] += d[i - 1][idx--];
			d[i][j] %= 10007;
			/*
				7로 예를 들어보면
				현재 i번째 자릿수의 숫자가 7이라면
				i-1번째 올 수 있는 수는 7, 8, 9로 3개이다
				즉, d[i][7] = d[i-1][7] + d[i-1][8] + d[i-1][9]
			*/
		}
	}

	ll ans = 0;
	for (int i = 0; i < 10; i++)	//0~9까지의 가짓수를 전부 더하는 연산
		ans += d[n][i];
	ans %= 10007;
	cout << ans;
}

다른풀이

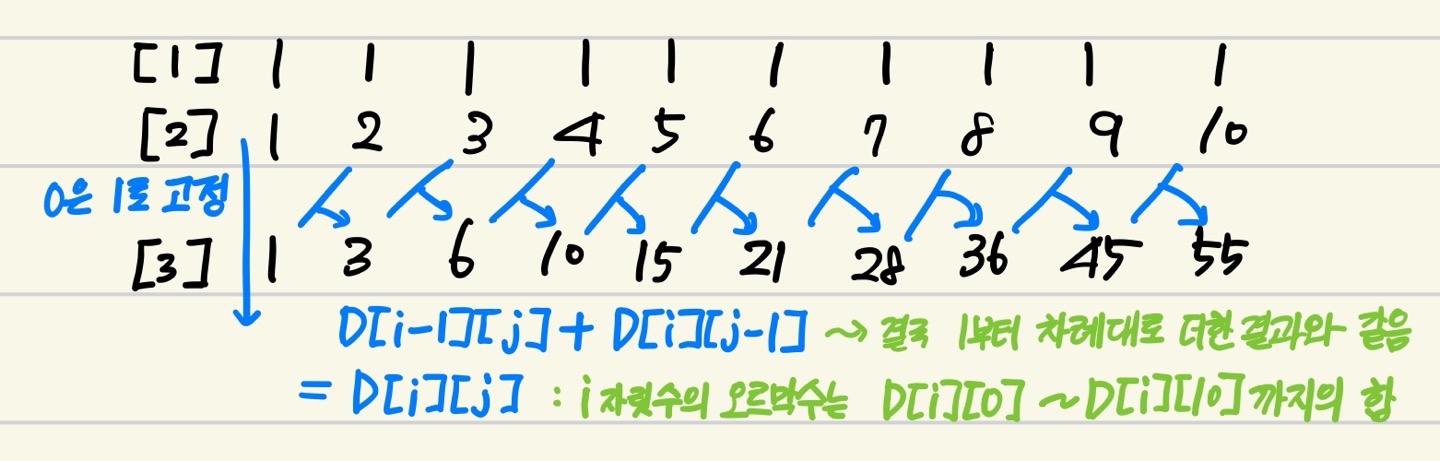
0~10까지의 테이블을 채울 때 3중 for문이 아니라 2중 for문으로 해결하는 방법

#include <bits/stdc++.h>
using namespace std;

const int N = 1003;
long long dp[N][10];

int main(void) 
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	int n; 
	cin >> n;

	for (int i = 1; i <= n; ++i) 
	{
		dp[i][0] = 1;
		for (int j = 1; j < 10; ++j)
			dp[i][j] = (dp[i][j - 1] + dp[i - 1][j]) % 10007;
	}

	/*
		accumulate : 배열의 합을 구하는 함수
		(first iter, second iter, 초기값)
	*/
	cout << accumulate(dp[n], dp[n] + 10, 0) % 10007;
}