백준 11729번 - 하노이 탑 이동 순서

문제

백준 11729번 문제

세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.

1. 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
2. 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.

이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.

아래 그림은 원판이 5개인 경우의 예시이다.

입력

첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.

출력

첫째 줄에 옮긴 횟수 K를 출력한다.

두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.

예제 입력 1 복사

3

예제 출력 1 복사

7
1 3
1 2
3 2
1 3
2 1
2 3
1 3

5-1. 정답코드

하노이 탑이 옮겨지는 과정

n개의 원판을 옮길 때	n-1개의 원판을 기둥 2로 옮김

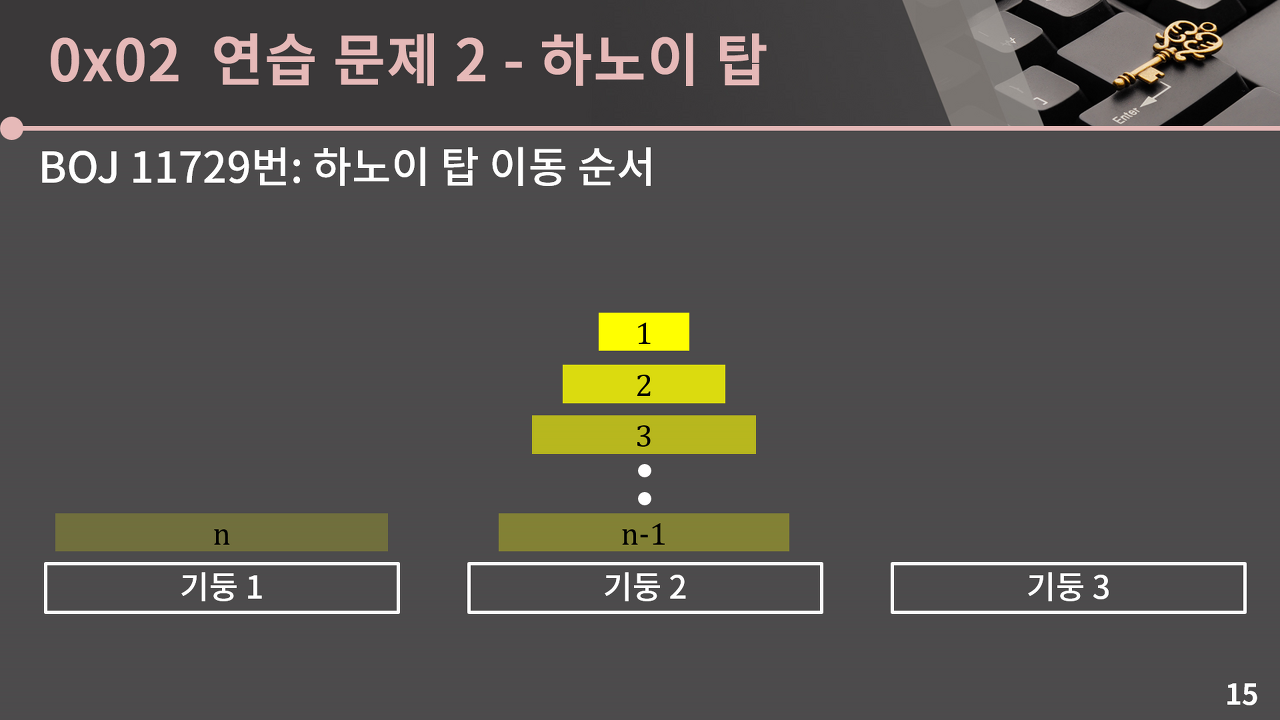| n번째 원판을 기둥3으로 옮김 | n-1개의 원판을 기둥 3으로 옮김 | |:————————————:|:————————————:| | | |

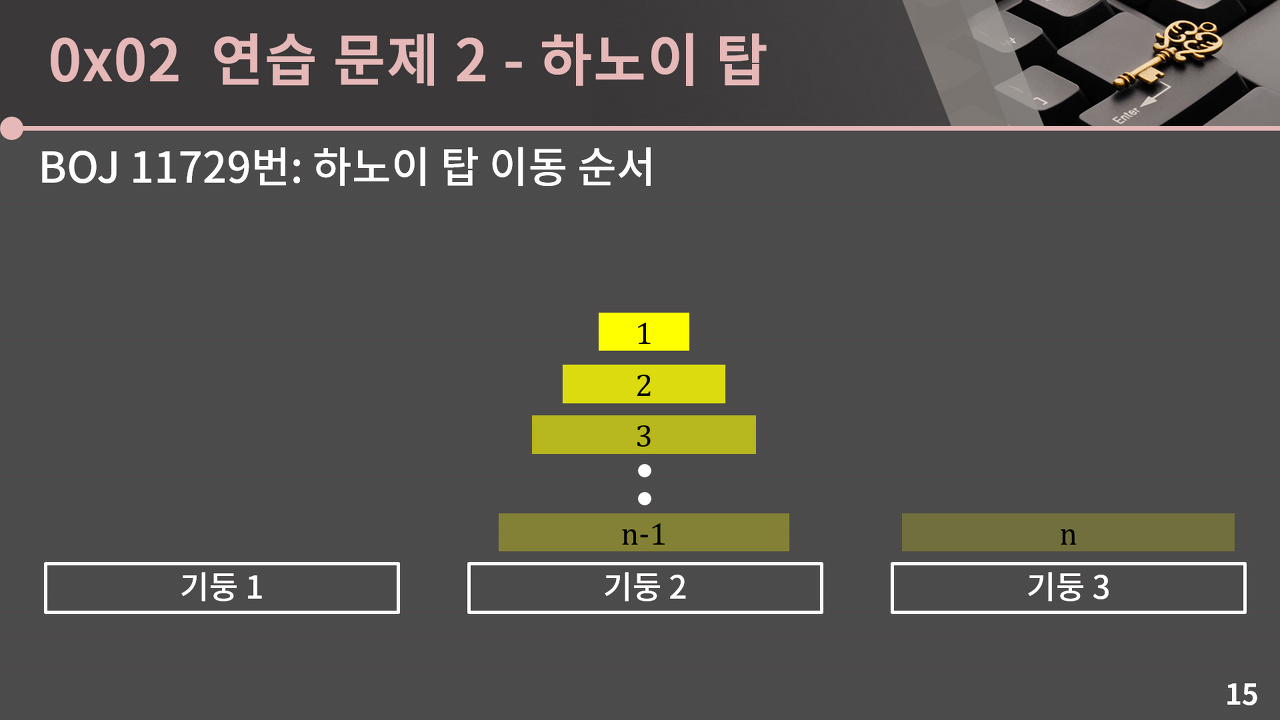절대 절차적인 접근을 해서는 안됨
절차적 접근을 하는 순간 끝이 없다. 수학적 귀납법으로 접근해야 한다.

1. 원판 1개를 내가 원하는 곳으로 옮길 수 있다.
   
   
2. n번째 원판을 옮기기 위해서는 n-1번째 원판을 옮겨야 함.
   거꾸로 말하면 n-1번째 원판을 옮길 수 있다면 n번째 원판을 옮길 수 있다.
   -> 원판이 k개일 때 옮길 수 있다고 가정하면 k+1개일 때에도 옮길 수 있다.
   
   2가지로 귀납법이 성립하고 재귀로 접근할 수 있다

함수 구조

이해가 안가겠지만 귀납적으로 이해를 해야한다
또한, 재귀함수는 맞게 호출된다고 믿고 써야 한다. 이게 진짜 맞는지 검증을 하려고 하면(절차적인 검증) 답이 없어진다

#include <bits/stdc++.h>
using namespace std;

void hanoi(int a, int b, int n)
{
    //n이 1개일때는 그냥 원판을 옮길 수 있음
    if (n == 1)
    {
        cout << a << " " << b << '\n';
        return;
    }

    //6은 기둥 1+2+3 의 합
    //1. n-1개의 원판을 a기둥에서 b가 아닌 다른 기둥으로 옮김
    hanoi(a, 6 - a - b, n - 1);
    //2. 마지막 n번째 원판 1개를 a기둥에서 b기둥으로 옮김
    hanoi(a, b, 1);
    //3. n-1개의 원판을 a와b가 아닌 기둥에서 b 기둥으로 옮김
    hanoi(6 - a - b, b, n - 1);
}

int main(void)
{
    ios::sync_with_stdio(0);
    cin.tie(0);

    int n;
    cin >> n;

    //초항이 1이고 2A+1인 수열의 일반식 -> 보통은 몰라도 됨
    //(1<<k) -1 이라고 해도 같다 2^k 승
    long long result = pow(2, n) - 1;
    cout << result << '\n';
    hanoi(1, 3, n);
}